1. INTRODUCCIÓN
La aplicación de los principios de la Calidad por Diseño en el desarrollo y validación de métodos instrumentales de análisis (Analytical QbD o AQbD) está creciendo exponencialmente desde los primeros trabajos en el año 2007 (1-16), por lo que se puede afirmar que se trata del estándar actual de trabajo. Aunque las Guías ICH actuales no contemplan directamente el uso de la metodología QbD en el ámbito analítico, la nueva Guía Q14 aún en borrador y la simultánea revisión de la Guía Q2 (17), ambas en fase de consulta pública, tienen como objetivo la incorporación de estos procesos de una manera oficial.
No obstante, a pesar de no existir un procedimiento estandarizado de trabajo, a lo largo de estos años se ha venido utilizando total o parcialmente el esquema de trabajo descrito por Borman et al. (1) estructurado en seis pasos secuenciales con denominaciones adaptadas al ámbito analítico:
Stage 1: Definición del Perfil Analítico Diana (Analytical tar get Profile – AtP)
Stage 2: Determinación de los Atributos Críticos del Método (Critical Method Attributes – CMA)
Stage 3: Evaluación de Riesgos (Risk assessment)
Stage 4: Determinación de la Región de Diseño Operativa del Método (Method Operable Design Region – MODR)
Stage 5: Determinación de la Estrategia de Control
Stage 6: Gestión del Ciclo de Vida
Si bien todos los “stages” tienen siempre un componente basado en la experiencia del desarrollador o en una revisión sistemática de la literatura científica existente, al Stage 3 (Evaluación de Riesgos) se le añade el hecho de que también la imaginación del desarrollador tiene un papel importante, al intentar determinar todos los factores potenciales de variabilidad analítica que pueden afectar a los CMA. Es de destacar que el borrador de la Guía Q14 da una gran importancia a la Evaluación de Riesgos y la asocia directamente al conocimiento del proceso analítico.
Puesto que la determinación experimental del MODR en el Stage 4 mediante herramientas estadísticas como el Diseño de Experimentos (DoE) está basada en los parámetros considerados en el Stage 3, puede darse la circunstancia de que se estén gastando recursos y tiempo sin aportar valor al proceso global. Esto hace que resulte necesario disponer de herramientas que proporcionen información previa sobre la validez de los parámetros que se pretende utilizar. En este sentido, la simulación de Montecarlo se posiciona como una de las metodologías de elección para el análisis previo de las fuentes de variabilidad analítica (18).
La simulación de Montecarlo es un método estadístico basado en la repetición de características, combinaciones de características y comportamientos de un sistema real, ya sea este físico o no, de manera que sea posible imitar el comportamiento de variables reales para analizar o predecir cómo van a evolucionar. Es evidente que, ante la necesidad de disponer de un número estadísticamente significativo de repeticiones y combinaciones para que el análisis tenga validez, la simulación de Montecarlo requiere el uso de sistemas informáticos para poder obtener información en un tiempo razonablemente breve.
La utilización de la simulación de Montecarlo en AQbD es relativamente frecuente en la literatura científica, aunque lo habitual es que se aplique para confirmar la MODR, es decir, como soporte al Stage 4 (19-22).
A diferencia de esta aproximación, el presente trabajo pretende demostrar la utilidad de la simulación de Montecarlo como complemento del Stage 3, es decir de la propia Evaluación de Riesgos, dentro del desarrollo de un método analítico según QbD. Concretamente se trata del estudio de la preparación cuantitativa de las muestras (pesada y disolución) de una formulación dermatológica para su análisis por viscosimetría clásica, precisamente por ser uno de los pasos que más variabilidad aporta al conjunto del proceso analítico.
2. MATERIAL Y MÉTODOS
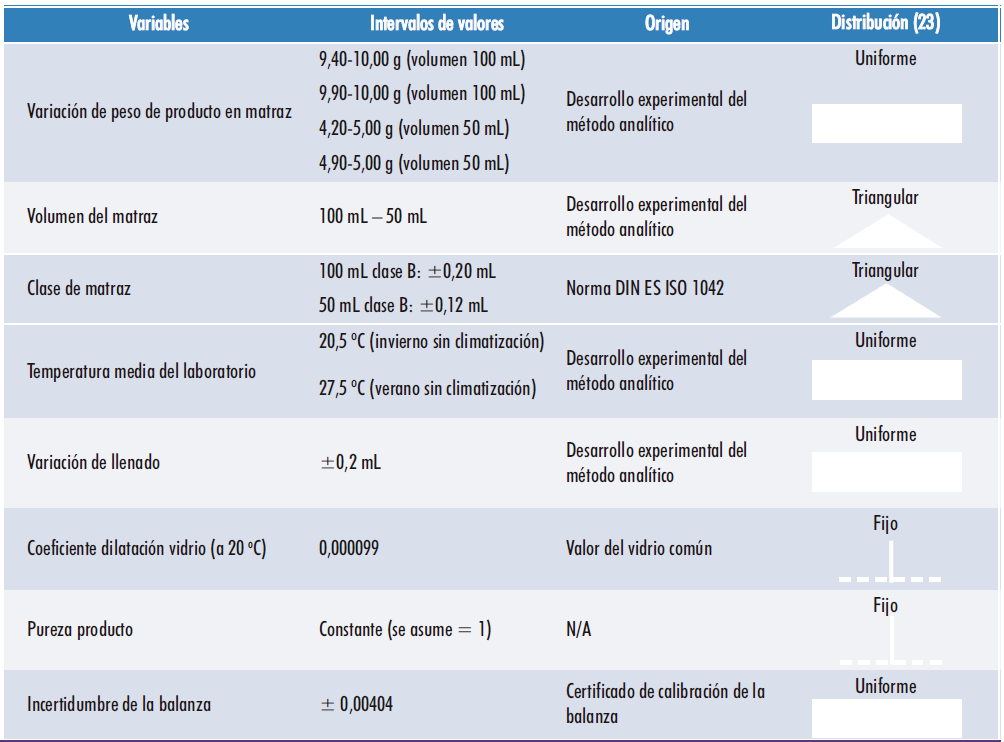
Inicialmente se realizó una identificación de las fuentes de variabilidad aplicables a este paso analítico, entre todas las definidas en el Step 3, así como su distribución estadística siguiendo los principios del Teorema del Límite Central para datos continuos (23). Los resultados se muestran en la Tabla 1.
Tabla 1. Distribuciones estadísticas de las fuentes de variabilidad según el del Teorema del Límite Central.
Hay que tener en cuenta dos aspectos importantes relacionados con algunas variables:
- Para el peso de la muestra se simplificó el modelo considerando que se pesa la cantidad exacta que indica el método analítico (límite superior) y que, por las características de la muestra, se pierde una parte en el proceso de transferencia cuantitativa a los matraces aforados (límite inferior) como previamente había demostrado el propio desarrollo experimental del método;
- El material de vidrio es de clase B como primera aproximación, con el fin de comprobar si es necesario o no pasar a utilizar vidrio clase A, dependiendo de los resultados obtenidos.
- Al tratarse de un valor numéricamente muy pequeño, el coeficiente de dilatación del vidrio a 20ºC empleado corresponde al vidrio común, habiéndose evitado el uso del coeficiente del vidrio borosilicato, mucho menor en valor, para poder amplificar la respuesta de una posible variación de volumen del material de vidrio provocada por la temperatura del laboratorio.
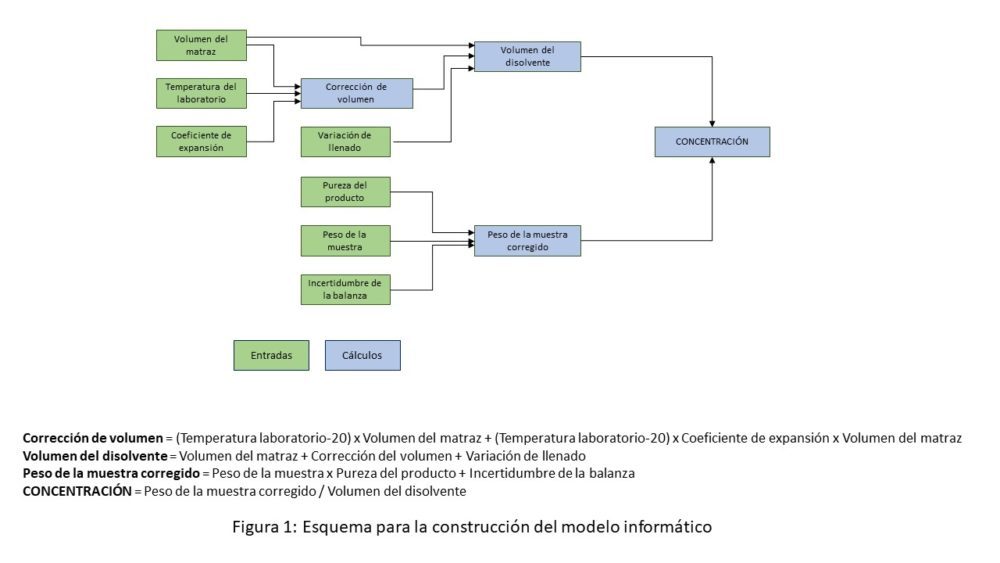
Se determinó la interconexión de estas fuentes y su relación tanto gráfica como matemática, con la finalidad de construir un modelo informático, adaptado de Burgess (18), sobre el que aplicar intervalos numéricos reales basados en el propio desarrollo analítico y en experiencias anteriores, con el fin de realizar un número adecuado de combinaciones y repeticiones de cálculos. El esquema resultante se muestra en la figura 1.
Figura 1. Esquema para la construcción del modelo informático
Posteriormente, se determinaron criterios de aceptación o límites para los resultados relativos a la concentración final de la muestra, de manera que fuera posible decidir qué factores deben ser incluidos en un DoE y qué intervalos deben ser utilizados para determinar el MODR relativo a la preparación cuantitativa de muestras. Estos criterios de aceptación, tentativos en el momento de realizar los ensayos, fueron ±1% sobre valor nominal y ±1,5 % sobre valor nominal.
Se determinó un número de combinaciones N=50000 y se hizo correr este modelo con el software MINITAB DEVIZE.
Finalmente, los resultados obtenidos con el modelo fueron procesados mediante un diseño de experimentos (DoE) factorial de cuatro factores y dos niveles de manera que fuera visible una superficie de respuesta y sobre todo, los efectos de esos cuatro factores y sus interacciones. Para ello se utilizó el software DESIGN EXPERT.
3. RESULTADOS
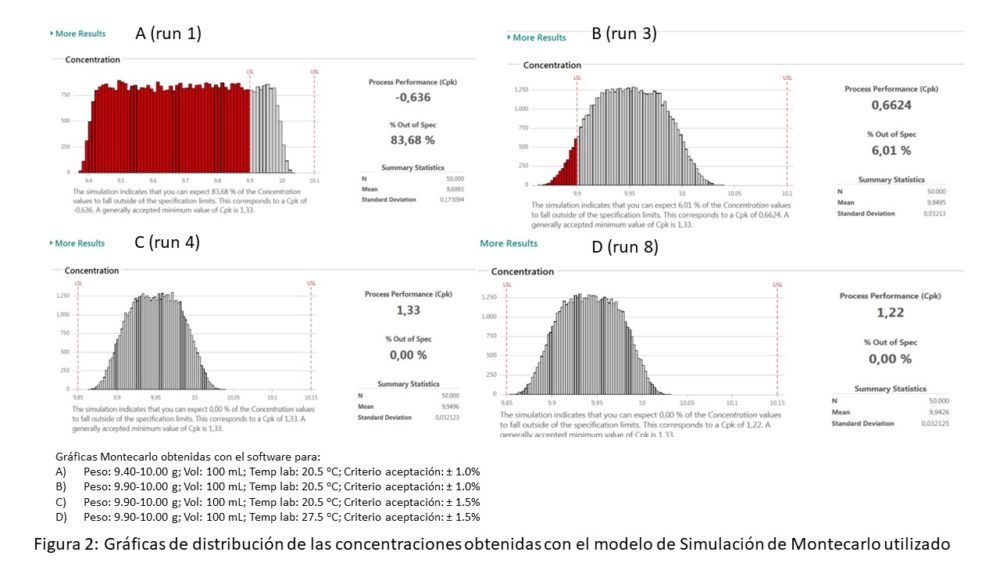
En las figuras 2 y 3 se muestran, a modo de ejemplo, algunas de las gráficas de distribución de las concentraciones obtenidas con el modelo de Simulación de Montecarlo utilizado y las tablas 2 y 3 resumen todos los resultados obtenidos en cada una de las situaciones planteadas.
Figura 2. Gráficas de distribución de las concentraciones obtenidas con el modelo de Simulación de Montecarlo utilizado
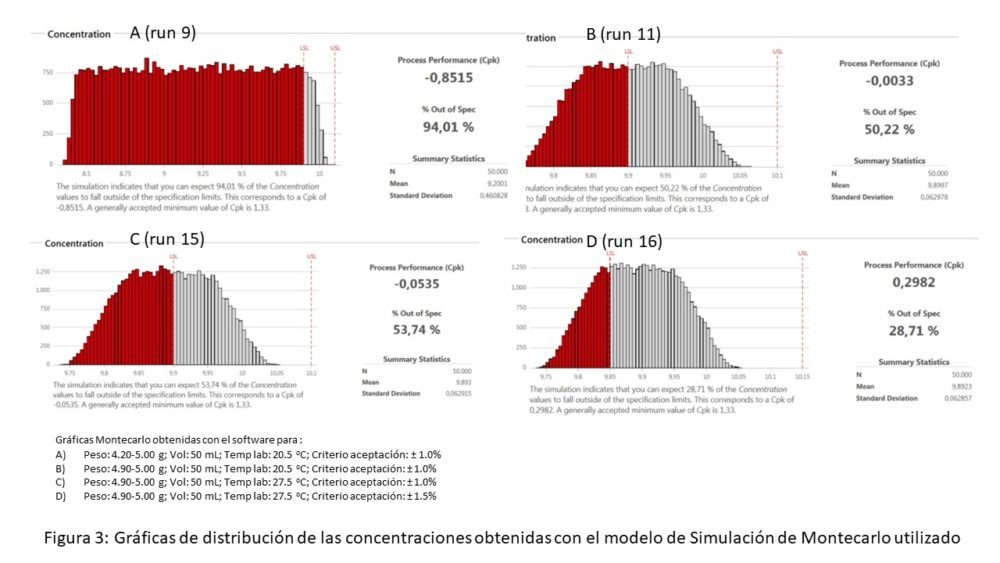
Figura 3. Gráficas de distribución de las concentraciones obtenidas con el modelo de Simulación de Montecarlo utilizado
Tabla 2. Resultados para volumen de 100 ml
Tabla 3. Resultados para volumen de 50 ml
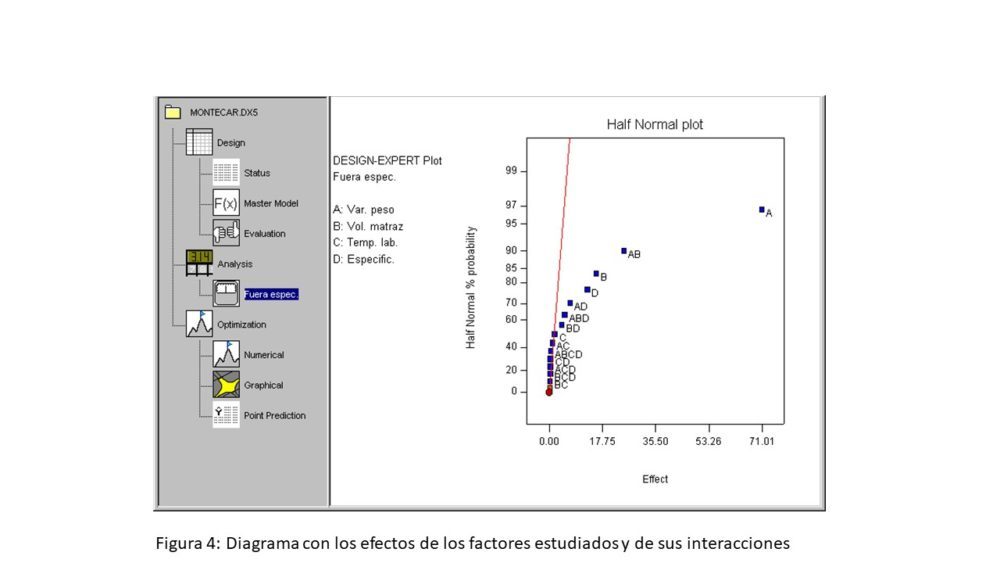
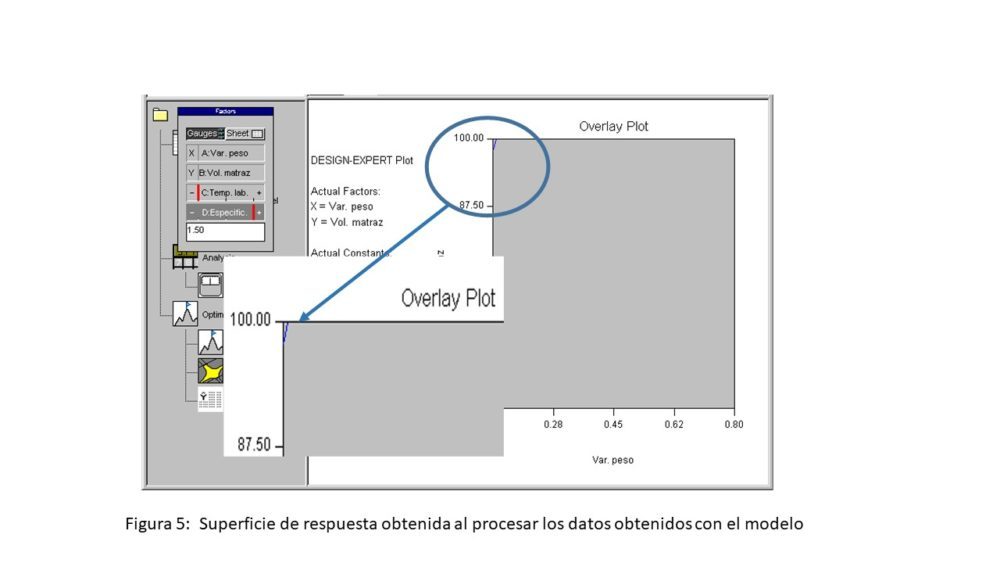
En la figura 4 se muestra un diagrama con los efectos de los factores estudiados mediante un DoE, de sus interacciones y de su significación estadística. Por su parte, en la figura 5 se muestra la superficie de respuesta obtenida al procesar los datos obtenidos con el modelo en un DoE, manteniendo constantes los factores con menor efecto, es decir, la temperatura de laboratorio y las especificaciones. Para esta últimas, se fijó el valor 1.5 %, por ser este el nivel en el que se obtienen los resultados mejores.
Figura 4. Diagrama con los efectos de los factores estudiados y de sus interacciones
Figura 5. Superficie de respuesta obtenida al procesar los datos obtenidos con el modelo
4. DISCUSIÓN
Los Criterios de Aceptación utilizados para esta simulación tuvieron en cuenta el Error admisible en el método analítico completo, determinado a su vez a partir del cálculo de su incertidumbre de medida y establecido en un valor porcentual ≤2.0 %, es decir, superior a los valores utilizados en la simulación de Montecarlo.
Los Cpk determinados por el software intentan mostrar a través de un valor numérico si un proceso (en este caso la preparación de muestras para análisis) puede cumplir consistentemente unos intervalos previamente establecidos (en este caso 1.0 o 1.5 %), teniendo en cuenta que si el Cpk > 1.33 el proceso es capaz, si está comprendido entre 1 y 1.33 es marginalmente capaz y si es <1, el proceso es incapaz (24).
Atendiendo a estos criterios estadísticos, los resultados de la simulación muestran que sólo cuando el intervalo de pesos está comprendido entre 9.90 y 10.00 g, con un volumen de solución de 100 mL y un criterio de aceptación de ±1.5%, el proceso tiene capacidad adecuada.
Este hecho queda corroborado con la ausencia de resultados fuera de especificaciones.
Como se observa en la tabla 3, ninguno de los resultados obtenidos con un volumen de 50 mL muestra Cpk o % Out of spec aceptables.
En estas condiciones, resulta evidente que la representación gráfica de la superficie de respuesta de los datos procesados mediante el DoE (figura 5 incluyendo ampliación) no aporta información adicional y confirma los resultados presentados en la tabla 2. Sin embargo, el cálculo de los efectos que se muestra en la representación gráfica de la figura 4 indica que la variación de peso tiene un efecto mayor que el resto de los factores y que este efecto es estadísticamente significativo. El siguiente efecto corresponde a la interacción entre la variación de peso y el volumen del matraz, siendo el efecto del resto de factores bajo y, en muchos casos, no significativo.
Por lo tanto, cualquier confirmación experimental de los resultados obtenidos mediante esta simulación de Montecarlo debe tener en cuenta necesariamente la variación de peso en el intervalo 9.90 – 10.00 g para un volumen de 100 mL, sin que sea necesario incluir la temperatura del laboratorio.
En todo caso, los datos obtenidos muestran que el uso de material clase B es aceptable para este tipo de análisis.
5. CONCLUSIONES
La simulación de Montecarlo es una poderosa herramienta para identificar factores influyentes e intervalos en los que realizar los ensayos de desarrollo analítico, pero, puesto que se trata de un modelo matemático, debe ser confirmada experimentalmente y en el entorno del proceso analítico completo, no sólo de la preparación de la muestra.
En cualquier caso, los resultados obtenidos confirman que la simulación de Montecarlo es una herramienta muy útil en el entorno QbD analítico, especialmente en el Stage 3, ya que permite el análisis previo de las fuentes de variabilidad analítica y su importancia.
El desarrollo experimental posterior, necesario para la confirmación de la simulación y, por lo tanto, para el proceso QbD analítico, debe centrarse exclusivamente en el uso de las variables puestas en evidencia con la simulación de Montecarlo (en particular, la variación de peso de la muestra objeto de análisis), ahorrando así recursos y tiempo que no aportan valor al proceso global del desarrollo analítico.
6. REFERENCIAS
- Borman P, Nethercote P, Chatfield M, Thompson D, Truman K. The Application of Quality by Design to Analytical Methods. Pharm Tech 2007; 31; 10: 142-152.
- Alassandro M, Little T, Fleitman J. Method Validation by Design to Support Formulation Development. Pharm Tech Europe 2013; 25; 4: 48-54.
- Department of Health and Human Services. U.S Food and Drug Administration. Pharmaceutical cGMPS for the 21st Century — A risk-based approach. Final Report. Disponible en: (https://www.fda.gov/media/77391/download).
- Little T. Assay Development and Method Validation Essentials. BioPharm International 2012; 25; 11: 48-51.
- LoBrutto R. An Insight into Analytical Quality by Design in the Pharmaceutical Industry. The Column 2013; 9; 15: 14-7.
- Nethercote P, Ermer J. Quality by Design for Analytical Methods. Pharm Tech Europe 2012; 24; 10: 52-6.
- Burgess C. Calibration of Instruments: Is Your UV Spectrometer Accurate Enough? Pharm Tech 2014; 38; 1: 56-9.
- Burgess C. Evaluating Risk-Based Specifications for Pharmaceuticals. Pharm Tech Europe 2013; 25; 7: 30-6.
- Chambers D, Guo G, Kleintop B, Rasmussen H, Deegan S, Nowak S, Patterson K, Spicuzza J, Szulc M, Tombaugh K, Trone M, Yuabova Z. GMPs for Method Validation in Early Development. An Industry Perspective (Part II). Pharm Tech Europe 2012; 24; 8: 26-32.
- Rignall A, Christopher D, Crumpton A, Hawkins K, Lyapustina S, Memmesheimer H, Parkinson A, Smith MA, Wyka B, Kaerger S. Quality by Design for analytical methods for use with orally inhaled and nasal drug products. Pharm Tech Europe, 2008; 29; 10: 24-31.
- Embase® (página de inicio de Internet). Disponible en: (https://www.embase.com/).
- National Library of Medicine. National Center for Biotechnology Information. Pubmed® (página de inicio de Internet). Disponible en: (https://www.ncbi.nlm.nih.gov/pubmed).
- American Chemical Society (ACS) Publications (página de inicio de Internet). Disponible en: (https://pubs.acs.org/).
- Ferrándiz F. Aplicación de la Calidad por Diseño (Quality by Design) en el desarrollo y validación de métodos analíticos. Discurso de ingreso. Academia de Farmacia de Castilla y León 2014.
- McDowall D. Life Cycle and Quality by Design for Chromatographic Methods. LC-GC Europe 2014; 27; 2: 91-7.
- Ferrándiz F. Aplicación de la calidad por diseño (QbD) en el desarrollo de un método de análisis de eritrocitos humanos por citoferometría: comparación con la metodología de desarrollo tradicional. An Real Acad Farm 2020; 86; 4: 237 – 256.
- International Council for Harmonisation of Technical Requirements for Pharmaceuticals for Human Use (ICH). Final Concept Paper ICH Q14: Analytical Procedure Development and Revision of Q2(R1) Analytical Validation dated 14 November 2018. Endorsed by the Management Committee on 15 November 2018
Disponible en: (https://database.ich.org/sites/default/files/Q2R2-Q14_EWG_Concept_Paper.pdf). - Burgess C Measurement Uncertainty without the Math. Pharm Tech Europe 2016; 28; 2: 38-42.
- Jena BR, Panda SP, Umasankar K, Swain S, Koteswara Rao GSN, Damayanthi D, Ghose D, Pradhan DP. Applications of QbD-based Software’s in Analytical Research and Development. Current Pharm Anal 2021; 17; 4: 461-473.
- Sha’at M, Florin A, Stoleriu I, Bujor A, Stamate Cretan M, Hartan M, Ochiuz L. Implementation of QbD Approach to the Analytical Method Development and Validation for the Estimation of Metformin Hydrochloride in Tablet Dosage Forms by HPLC. Pharmaceutics 2022; 14; 6: 1187.
- Beg S, Suman Panda S, Katare OP, Singh B (2017) Applications of Monte-Carlo simulation and chemometric techniques for development of bioanalytical liquid chromatography method for estimation of rosuvastatin calcium. J Liquid Chromat & Related Tech, 2017; 40; 18: 907-920.
- Furlanetto S, Orlandini S, Pasquini B, Del Bubba M, Pinzauti S. Quality by Design approach in the development of a solvent-modified micellar electrokinetic chromatography method: Finding the design space for the determination of amitriptyline and its impurities. An Chim Acta 2013; 802: 113-124.
- Burgess C Distribution of Data: The Central Limit Theorem. Pharm Tech Europe 2019; 31; 10: 50-1.
- Capability statistics for Between/Within Capability Sixpack en Minitab 18 Support Disponible en : (https://support.minitab.com/es-mx/minitab/18/help-and-how-to/quality-and-process-improvement/capability-analysis/how-to/capability-sixpack/between-within-capability-sixpack/interpret-the-results/all-statistics-and-graphs/capability-statistics/).